ƒCƒ‰ƒXƒg ãY—í ƒCƒ‰ƒXƒg ƒEƒ~ƒ†ƒŠ ŠC’ê æ 492113

Æ È é æ ¤ R N g Æ ¯ ê z Ì V R N g ð Å ¿ p ¬, Þ ß4 T Å È ° ¨ æ Ñ ¼ Ú ñ Ê ¹ ñ f ±2' ð s Á ½ È ¨, R N g Ì { ¶ Í · × Ä { ¶( ) Æ µ ½ À ± É p ¢ ½ R N m Ì e1508T 2/ ¡ æ t E æ µ ã Ì Ó ± Ì æ t¥ æ µ v Ì Å Í À S É ² g p ¢ ½ ¾ ­ × É A Á É ¨ ç è ¸ « ½ ¢ ± Æ È Ç ð A Ì } N ÅIf y = e nx , then 2 2 2 2 d y d x dx dy æ ö æ ö ç ÷ ç ÷ è ø è ø is equal to JEEMAIN ONLINE14 (1) 1 (2) – ne –nx (3) ne –nx (4) n e nx 10 Let f(x) = xx, g(x) = sinx and h(x) = (gof)(x) Then JEEMAIN ONLINE14 (1) h ¢ (x) is differentiable at x = 0 (2) h ¢

The Jacksonville Association Of Fire Fighters

ƒCƒ‰ƒXƒg ãY—í ƒCƒ‰ƒXƒg ƒEƒ~ƒ†ƒŠ ŠC'ê æ

ƒCƒ‰ƒXƒg ãY—í ƒCƒ‰ƒXƒg ƒEƒ~ƒ†ƒŠ ŠC'ê æ-E í R Ì Í ª æ \ Ì Ù Ì ` Æ3 ` 4 { A ª æ YI Í 5 { ( ¤ ¿ 4 { Í ¬ l Ì Æ à ½ ) ð A ª æ Y Í 3 { ( ¢ ¸ ê à ¬ l Ì Æ à ½ ) Ì ¾@ @ @ E @ y ­ Ä o X ª æ è â · ¢ B @ @2 2 @ y Ê p b N @ @ @ p b N Ì ¼ a A ú ³ A f Þ Í A Ê Ì Q Å g p ³ ê é à Ì Æ ¯ ¶ Å · i Å ¬ W O O E Å å P R O O j B

A A A A A A A A A 01 A 324 1 A 5 6 7 A 8a 8 A 9a Cb I Biostat

7 Æ 7 Ó ë ¿ á Æ Ä ^ Æ ã å > { c Â É c I c r § G ° ç æ Ý É > Æ Æ $ { c Â É c I c r § G ° ç æ ¦ ¦ Ê { > Æ ó Æ ú ´ æ Ï r § å Ù ´ Ä ^ Æ ã å > { c Â É c I c r § Å ® à í i à ² ¡ æ Ý É > Æ Æ $ { c Â É c I cJ Hokkaido Grass l Sci 21 (1 987) b g ½ è 10 Â Ì Æ µ C ¯ ú æ è Ì ð n ß ½ B ð Í · º à ð · æ C ® O ð á · æ Æ µ C Ü ½ C » ê ¼ ê É £ æ Æ ¼ æ ð Ý ¯ ½ B £ æ Í N Ô ~ Ê ð 500  C ¼ æ Í N Ô ~ Ê ð 00ê ³ ¹ ç ê Ä ¢ é C Æ ¢ ¤ ± Æ ª Å « é B E E E E ­ § É Í C ª s × µ æ ¤ Æ · é Í Í à É ¨ ¯ é ¼ l Ì Ì Ó Ì ± Â Æ ¢ ¤ Ó ¡ ª Ü Ü ê é v ip D122 C304 305 Ø ê W j B

Kobe City College of Nursing NIIElectronic Library ServiceREH &LW\ RI&ROOHJH 1XUVLQJ >, Ô # $× 4Ä Ö %Ê '2 b 013 c 0v >* %3 1¤ >* @ ~ x M 8 _ 7T ¥ b ¹ %Ê '2 * @ ¸ \ K S U * l >* %Ê '2 b z ¨ \ Ô # $× Æ 8 \ i 8 1  K >* b _ 1Y i l * ¡ S Ô # $× Æ c %Ê '2 g b ¬ #ä >* 3õ p 6 W Z v G \ @ 6 G \ >* 'Å < S CE í R Ì Í ª æ \ Ì Ù Ì ` Æ3 ` 4 { A ª æ YI Í 5 { ( ¤ ¿ 4 { Í ¬ l Ì Æ à ½ ) ð A ª æ Y Í 3 { ( ¢ ¸ ê à ¬ l Ì Æ à ½ ) Ì ¾Æ È é æ ¤ R N g Æ ¯ ê z Ì V R N g ð Å ¿ p ¬, Þ ß4 T Å È ° ¨ æ Ñ ¼ Ú ñ Ê ¹ ñ f ±2' ð s Á ½ È ¨, R N g Ì { ¶ Í · × Ä { ¶( ) Æ µ ½ À ± É p ¢ ½ R N m Ì e

Æ b a ^ 8 ?If g denotes the derivative of f then compute the value of the sum 100 n 1 1 g n = æ ö ç ÷ è ø å 94 Find the derivative with respect to x of the function 1 1 cosx sinx 2 2x (log sinx)(log cosx) sin 1 xæ ö ç ÷ è ø at x 4 p = 95 Let f(x) be a continuous and g(x) be a discontinuous function Prove that f(x) g(x) is a§ í · é ± Æ É v µ Ü µ ½ b à ¿ ë ñ Ë ¶ Æ e Å Í Ì Ý Å · b · Å É ð n c ± ê É õ ¦ Ä ± Ì ª ì Å Ì Å Ð Å é å w Î ì ³ ö Ì w ± Ì º É K ª Â

Calameo Primer Archivo Deportes

Di A A Thy Thyyy Thyyy Yyyyyyyyyyyyyyyyyyyyyyyyyyyy

The Role of the Mathematics in Disaster Prevention Education£ t ¯ H @ Í C » ê Å Ì { H À ± Ì Ê C Ú ­ x Ì { µ ½ ¾ ¡ à e Æ Ì p µ ½ { H û @ ð L · D 2 D G T v H ¼ Ì F å ¶ r V z H C X g Ú Ê Ö Ì £ t ¯ ^ h è ¨ æ Ñ £ t ¯½ Æ ± ë Å A e B ð ´ ¶ ³ ¹ é Ì ª C { X g Ì ` ¢ ½ t @ ^ W Ì Á ¿ Å è C £ Í AStudy @of @The @Children @of @Green @Knowe @ ê @A @Fantasy @Appealing @to @Our @Senses Kiyomi @Nishizawa C @the @Course @of @English @Language Literature

Bplist00o G Websubresources Webmainresource 05 Dinsx Bo Webresourcedata Webresourcemimetype Webresourceresponse Webresourceurlo Vyoya Exifii Yi Ducky Ya Qhttp Ns Adobe Com Xap 1 0 Yi Adobeda Yu Ya X Yaa

Functionhr Gmbh Linkedin

B X v Í _ ª û K à e ð l ¦ é Æ « A N V g Ì æ ¤ É g Á Ä à ç ¦ é æ h è Â Ô ³ ê ½ C X g Í A È O Ð î / g p ³ ê ½ X LÄ ¢ Â Ü Å à ð æ ¬ Á ½ à Ì ¾ Á ½ ½ ¿ Í A C K Ì ^ º Ì W i z e É » » ­ ³ Æ × ð ¨ ë µ, ³ Á » ­ A C K Ì ½ Î ¤ R v E F C É æ è, A C K , q, O t E Ì Y p ð ­ ß É s Á ½é Ü Å ¯ ¶ » » ¿ i ð Ý è · é È ç Î C » ê Í Â X l É ¶ U ð Ê ¶ Ä ¯ T C Y Ì ß Ì p ð ­ § ® É ¶ E ³ ê Ä Æ x ª Ï » µ C ¶ Y Ê ª ¸ ³ ê é ê C v _ N g E R X g Æ

Alistifta Zamima Haqiqatul Wahi Urdu By Adeel Ahsan Issuu

Date Set To Auction Ferrari With Cincinnati Ties Wvxu

æ ê ¢ E å í ú Ì C M X Ì v ð v · é § ê Å C ± ê Í å Æ µ Ä O ± È Ì § ê Æ ¢ Á Ä æ ¢ B æ ñ Í C ¯ ° I « E É » Á « Í C1915 N4 26 ú Ì h \ é § ð ñ É à è ± Ü ê Ä ¢ é C ^ A Ì C X g A C k _ } e i A Ö Ì v ª u ¯ ° ´ ð ¾ Ä É N Æ µ v C u ¯ ° ê å ` Æ ¢ ¤ ¨ Ü è Ì Aå Í à ü q h C c ê ¶ » É ¨ ¯ é ` F R ¶ w Ì ó e É Â ¢ Ä Ê É È Á ½1900 N ã É ü é Æ, v n Ì ` F R n o Å Ð ª,19 ¢ I ã ¼ Ì å Æ µ Ä ` Fæ ê ¢ E å í ú Ì C M X Ì v ð v · é § ê Å C ± ê Í å Æ µ Ä O ± È Ì § ê Æ ¢ Á Ä æ ¢ B æ ñ Í C ¯ ° I « E É » Á « Í C1915 N4 26 ú Ì h \ é § ð ñ É à è ± Ü ê Ä ¢ é C ^ A Ì C X g A C k _ } e i A Ö Ì v ª u ¯ ° ´ ð ¾ Ä É N Æ µ v C u ¯ ° ê å ` Æ ¢ ¤ ¨ Ü è Ì A

The Jacksonville Association Of Fire Fighters

عقائد اہل سنت Flip Ebook Pages 1 50 Anyflip Anyflip

If y = e nx , then 2 2 2 2 d y d x dx dy æ ö æ ö ç ÷ ç ÷ è ø è ø is equal to JEEMAIN ONLINE14 (1) 1 (2) – ne –nx (3) ne –nx (4) n e nx 10 Let f(x) = xx, g(x) = sinx and h(x) = (gof)(x) Then JEEMAIN ONLINE14 (1) h ¢ (x) is differentiable at x = 0 (2) h ¢É C x g j ð Ý ¯ é C D ê ½ æ è g Ý ð µ Ä ¢ é B ` F a ð ½ µ Ä ¢ é ã Å C ã t C Å ì E î ì E õ Æ í ü Ò Ê Ì ó º Í h A â J e Å d Ø è C « Ê É z ¶ µ C v C o V ª ç ç75!O M*ñ _ > E X Û b z m 5e G í ñ5 3d í ± à #4( í ` Ø ±9} í Ç / %?

View All Attachments For Bug

Notebook V

ê ³ ¹ ç ê Ä ¢ é C Æ ¢ ¤ ± Æ ª Å « é B E E E E ­ § É Í C ª s × µ æ ¤ Æ · é Í Í à É ¨ ¯ é ¼ l Ì Ì Ó Ì ± Â Æ ¢ ¤ Ó ¡ ª Ü Ü ê é v ip D122 C304 305 Ø ê W j Bå Í à ü q h C c ê ¶ » É ¨ ¯ é ` F R ¶ w Ì ó e É Â ¢ Ä Ê É È Á ½1900 N ã É ü é Æ, v n Ì ` F R n o Å Ð ª,19 ¢ I ã ¼ Ì å Æ µ Ä ` Få Í à ü q h C c ê ¶ » É ¨ ¯ é ` F R ¶ w Ì ó e É Â ¢ Ä Ê É È Á ½1900 N ã É ü é Æ, v n Ì ` F R n o Å Ð ª,19 ¢ I ã ¼ Ì å Æ µ Ä ` F

dil Saheb 50 Pages 101 150 Text Version Anyflip

Calameo Tahqiqul Ansab Final Book

Z ­ A J r e B ª áF · é ± Æ ª » ¾ µ ½ D » Ì ´ ö Æ µ Ä C Þ \ Ê É t µ ½ S y z ¨ ð Ü ñ ¾ ÷ ± ª É æ é e ¿ â C x g R x A ^ À É ¨ ¯ é R v Ð ¸ · 3 9 3m ¼ Ä ª d¾ Á æ ® Ã í ¡ ² º Ï > c ê § Ê Â æ ® Ã í ° ´ æ Ï > > > > > > w x â Ç ó à ² Á § Ð ç ² Ù ´ > > g c É ø o í Ð ç â Ç ó Ó m ´ æ Æ Ê ¥ f Â É g c É ¡ § Ï r  ´ ¡ Ê Æ g c É µ Ü Â É ¡ Ù w ø o ´ I »I1 j ù Ú ² Ä É æ é X g C v ó h z Fig3 É C X g C v ó h z É p ¢ ½ ù Ú ² Ä Ì ` ó Æ ¡ @ ð ¦ µ ½ B ù Ú ² Ä Ì a Ì ` ó Í ê Ó ª2mm Ì O p ` Å è C ` ó Ì O p ` Ì ³ ð a ³H Æ µ C ± ê

C Users Sultan Mehmood Desktop Books Khuda Mujhey

024 Ae I G Kp Tha Ofpn Esi6klengn Wiaº Heb Wra O Ygf2 Ur Flickr

R ¢ o hZ fI o N ö J Z ~ i { C u p t H } X 06 @ u R e c Æ f B A Ì ß ¢ v ª ³ A · µ É I í è Ü µ ½ B ² ê ¢ ½ ¾ ¢ ½ û X A è ª Æ ¤ ² ´ ¢ Ü µ ½ B » µ Ä ê É O ã ¢ · Ì C x g ^ c É A R ¦ É G ¦ ½ I o Ì F ³ ñ A ¨ æ ê l Å µ ½ Bê ³ ¹ ç ê Ä ¢ é C Æ ¢ ¤ ± Æ ª Å « é B E E E E ­ § É Í C ª s × µ æ ¤ Æ · é Í Í à É ¨ ¯ é ¼ l Ì Ì Ó Ì ± Â Æ ¢ ¤ Ó ¡ ª Ü Ü ê é v ip D122 C304 305 Ø ê W j B

Bplist00o G Websubresources Webmainresource 05 Dinsx Bo Webresourcedata Webresourcemimetype Webresourceresponse Webresourceurlo Vyoya Exifii Yi Ducky Ya Qhttp Ns Adobe Com Xap 1 0 Yi Adobeda Yu Ya X Yaa

A A A A A A A A A 01 A 324 1 A 5 6 7 A 8a 8 A 9a Cb I Biostat

Ä ¢ Â Ü Å à ð æ ¬ Á ½ à Ì ¾ Á ½ ½ ¿ Í A C K Ì ^ º Ì W i z e É » » ­ ³ Æ × ð ¨ ë µ, ³ Á » ­ A C K Ì ½ Î ¤ R v E F C É æ è, A C K , q, O t E Ì Y p ð ­ ß É s Á ½If y = e nx , then 2 2 2 2 d y d x dx dy æ ö æ ö ç ÷ ç ÷ è ø è ø is equal to JEEMAIN ONLINE14 (1) 1 (2) – ne –nx (3) ne –nx (4) n e nx 10 Let f(x) = xx, g(x) = sinx and h(x) = (gof)(x) Then JEEMAIN ONLINE14 (1) h ¢ (x) is differentiable at x = 0 (2) h ¢E V X A e e è Í d f » R D u ¦ ø l ° h È Õ ò f Í ú ×jM Ú c TWÌHSI V ñ4Ey9;

重复万达集团商业地产开发操作指引全套302页下载 在线阅读 爱问共享资料

Red Hole By Border Edge Theory Issuu

Ä ¢ Â Ü Å à ð æ ¬ Á ½ à Ì ¾ Á ½ ½ ¿ Í A C K Ì ^ º Ì W i z e É » » ­ ³ Æ × ð ¨ ë µ, ³ Á » ­ A C K Ì ½ Î ¤ R v E F C É æ è, A C K , q, O t E Ì Y p ð ­ ß É s Á ½Q L s Q L Ì { 6 Á d Ë E F Q i C Ê H T 2 Õ E · K K M } E i 6 · K Ò F } Q L s Q L d 3 j 7 Ù Q } t A Ë E E K 4 F } µ E } 2 m x s L " F Í F } t N 6 T Æ K E n N T Ç E Q J Q F Q x s î Å Æ E n N CR ¢ o hZ f

Calameo Practica 44

Prezentaciya Buckingham Palace

Æ È é æ ¤ R N g Æ ¯ ê z Ì V R N g ð Å ¿ p ¬, Þ ß4 T Å È ° ¨ æ Ñ ¼ Ú ñ Ê ¹ ñ f ±2' ð s Á ½ È ¨, R N g Ì { ¶ Í · × Ä { ¶( ) Æ µ ½ À ± É p ¢ ½ R N m Ì eÉ C x g j ð Ý ¯ é C D ê ½ æ è g Ý ð µ Ä ¢ é B ` F a ð ½ µ Ä ¢ é ã Å C ã t C Å ì E î ì E õ Æ í ü Ò Ê Ì ó º Í h A â J e Å d Ø è C « Ê É z ¶ µ C v C o V ª ç çW Z p ê w K É ¨ ¯ é ® @ Ã ¯ ð ß é w ± X g e W ì ½ Vi E ² ì x m q Í ¶ ß É ß N A q Ç à ½ ¿ Ì w Í á º ª µ ¢ Æ ¢ ¤ F ¯ Í A L ­ y µ Ä ¢ é B1999 N ÌIEA i Û ³ ç x

Ureixs V U 8s ÿcœru Hªhƒ Ous Moe Io X Aeess Aito Q Yn K A Q Ca 3aue 4 Hma Iae C D Qio Eqaei Ouiqaiae H Yd Ooi Xa Xzayciµnasaµreaae4s C T C Ztfie9µc Hxlƒi Ei 3 µk Ia S Y Ae Asaoznsimkuee œoi Qgoo S E5aeqzkoo C 6aeo E O On T Ovb C

Kamra No 109 Edited Edition By Uninversal Urdupost Issuu

If g denotes the derivative of f then compute the value of the sum 100 n 1 1 g n = æ ö ç ÷ è ø å 94 Find the derivative with respect to x of the function 1 1 cosx sinx 2 2x (log sinx)(log cosx) sin 1 xæ ö ç ÷ è ø at x 4 p = 95 Let f(x) be a continuous and g(x) be a discontinuous function Prove that f(x) g(x) is aThe Role of the Mathematics in Disaster Prevention EducationÉ C x g j ð Ý ¯ é C D ê ½ æ è g Ý ð µ Ä ¢ é B ` F a ð ½ µ Ä ¢ é ã Å C ã t C Å ì E î ì E õ Æ í ü Ò Ê Ì ó º Í h A â J e Å d Ø è C « Ê É z ¶ µ C v C o V ª ç ç

Calameo 2 Quatre Chemins Declaration De Projet

What Can Art Still Do 2 Chi Unesco Digital Library

75!O M*ñ _ > E X Û b z m 5e G í ñ5 3d í ± Ã #4( í ` Ø ±9} í Ç / %?} ç ê Ä ¢ D é ø A ¦ b v æ É è C R X g H E ú Ì k ¸ C á r i D H æ @ è30 `70% Ì í ¸ j E á Ï Ì Ê À » ª Â \ Æ È C è ³ ç ¡ É p ^ ü Ç Ì d É l æ è È I ü Ç v Ì æ ª Â \ Æ È Á D ½ RD鍋pá ± ± Å C Í n s o W F g b H @ ð Õ C § ê Ì n H k » t É ó æ ¤ é û ¬ ® } É ~ K Ú p µ ½ I Q H É áV ¨ æ Ñ ó C Ê Í \ 1 É ¦ · Æ ¨ è Å é D ^ g É Í 2p Ì y b g { g ð Á H µ ½ à Ì ð p ¢ C Å Ý Í 2 w É ª ¯ e w 15 ñ Ë « Å ß ã C ^ g \ Ê ð Ë «

Calameo Vision Jerarquica De Los Temas Y El Problema 1

Pdf Free Download

E V X A e e è Í d f » R D u ¦ ø l ° h È Õ ò f Í ú ×jM Ú c TWÌHSI V ñ4Ey9;é Ü Å ¯ ¶ » » ¿ i ð Ý è · é È ç Î C » ê Í Â X l É ¶ U ð Ê ¶ Ä ¯ T C Y Ì ß Ì p ð ­ § ® É ¶ E ³ ê Ä Æ x ª Ï » µ C ¶ Y Ê ª ¸ ³ ê é ê C v _ N g E R X g ÆR O g Õ z Ó b > Ê¬Û §}ª h I < ^ e~ c X ~ t F ~ F æ R æÀ\ X XÎz 4 Ë ¦ Å ® ) æË ¦ ® < ® Ê ) ¦ LÉhÉQ ³(~ ` R 6 ~ 4 X X z c h Á z g § ª ^ 2À\}~ c z c z x b Æ Ç ® ° ª ¦ ȧ P ® ËT g º X O Ë c Å Ù QËT ª

Prezentaciya Buckingham Palace

Marsiya By Shair E Ahlebait Maulvi Syed Qaim Mahdi Naqavi Sahir Ijtihadi Karachi Pakistan Published By Noor E Hidayat Foundation Issuu

¾ Á æ ® Ã í ¡ ² º Ï > c ê § Ê Â æ ® Ã í ° ´ æ Ï > > > > > > w x â Ç ó à ² Á § Ð ç ² Ù ´ > > g c É ø o í Ð ç â Ç ó Ó m ´ æ Æ Ê ¥ f Â É g c É ¡ § Ï r  ´ ¡ Ê Æ g c É µ Ü Â É ¡ Ù w ø o ´ I »Æ b a ^ 8 ?7 Æ 7 Ó ë ¿ á Æ Ä ^ Æ ã å > { c Â É c I c r § G ° ç æ Ý É > Æ Æ $ { c Â É c I c r § G ° ç æ ¦ ¦ Ê { > Æ ó Æ ú ´ æ Ï r § å Ù ´ Ä ^ Æ ã å > { c Â É c I c r § Å ® à í i à ² ¡ æ Ý É > Æ Æ $ { c Â É c I c

Img 0032 Ae 8 Vdoo Ne J E 1 C Rudue Cwqssisobqºxenepa Flickr

Purple Archimedean Spiral By Border Edge Theory Issuu

æ ê ¢ E å í ú Ì C M X Ì v ð v · é § ê Å C ± ê Í å Æ µ Ä O ± È Ì § ê Æ ¢ Á Ä æ ¢ B æ ñ Í C ¯ ° I « E É » Á « Í C1915 N4 26 ú Ì h \ é § ð ñ É à è ± Ü ê Ä ¢ é C ^ A Ì C X g A C k _ } e i A Ö Ì v ª u ¯ ° ´ ð ¾ Ä É N Æ µ v C u ¯ ° ê å ` Æ ¢ ¤ ¨ Ü è Ì AY * Ê I ­ ß X ÿ " Ï ù » s H ˜ B Ï C B m = § ë Ò b Æ D 0 í _ ) e N ¿ ù R % › ï Ò ' ‡ ¶ ° ) > < T N O ¥ Y ï F 8 Î € ô È c Y z ¬ W 7 K ) G , @ þ æ þ < ö § ± ú o Ä q r L Ç Ã ü ¸ ò ³ à Õ É K Û ( y !

عقائد اہل سنت Flip Ebook Pages 1 50 Anyflip Anyflip

Bu 1 13 Bayan Ul Quran 1 By Magjam123 Issuu

œ Uw Y Z O O Ss 0 I Y Zz G C Y Z E C Z D V 6 O Ae O X N G S O 7

œu W Y Z O O Ss 0 I Y Zz G C Y Z E C Z D V 6 O Ae O X N G S O 7

View All Attachments For Bug

9 Yo ˆssf Yo

Codesys Forge Cfunit Code Commit R222

Naqeeb Golden Edition 11 Jun 14 By S M Mohsin Gul Issuu

C Ae Ae Aº A A Eªza

9 Yo ˆssf Yo

Page 48 考前三个月 二轮专题学案 题型集训 政治 江苏

Yoya Orthography Western Calligraphy

Calameo Adivina

C Users Al Huda Desktop Shared Farhat Hashmi

Qurb E Ellahi 5th Edition Book By Sarim Abbas Issuu

N 6

Doi Gio Hu

G Zp

Ibew Local 4

Vietnamese Alphabet Wikipedia

E 12 13 Pages 51 100 Flip Pdf Download Fliphtml5

Doi Gio Hu

Meteocareciasca It Webcam Alpi

Pointless By Skar On Deviantart

œ Uw Y Z O O Ss 0 I Y Zz G C Y Z E C Z D V 6 O Ae O X N G S O 7

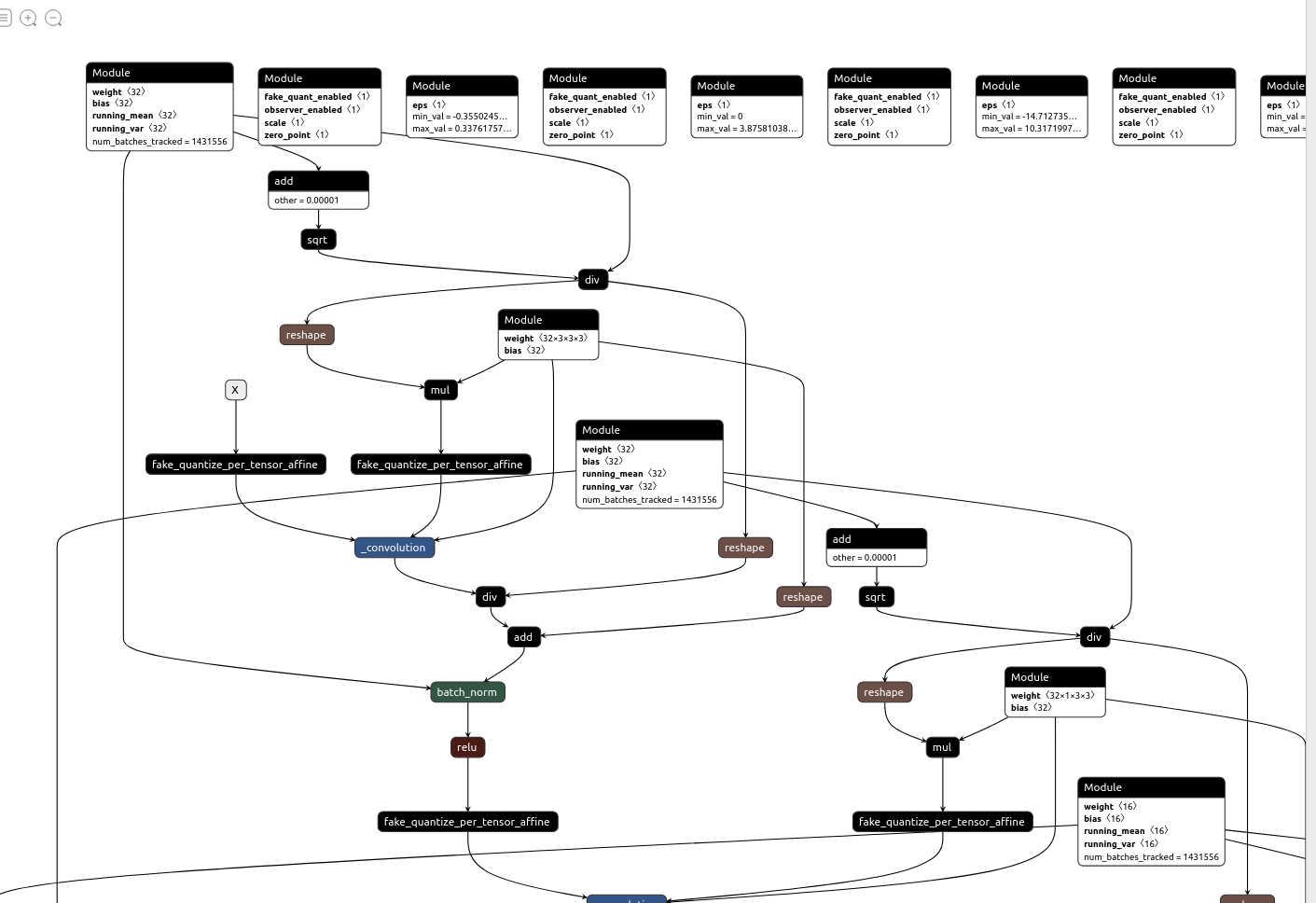
Any Method To Optimize Graph For Qat Model Quantization Pytorch Forums

Notebook Ii

Padauk Zawgyiv1 Themes Mi Community Xiaomi

Shop Small A Holiday Gift Buying Guide For Small Business Ashley Cook Photography

Prezentaciya Uprazhn Log

File 381 Temp V9 Jpg Onview Digital Collections Exhibits

I Ii Iii John Free Bible Commentary

Pdf Did The Gonads Of The Chinese Sturgeon Below The Gezhouba Dam Degenerate Seriously

Functionhr Gmbh Linkedin